 Quando scrivo la lettera Q non faccio altro che configurare una serie di circuiti in modo che poi sullo schermo compaia proprio la lettera Q.
Quando scrivo la lettera Q non faccio altro che configurare una serie di circuiti in modo che poi sullo schermo compaia proprio la lettera Q.
In ultimissima analisi quindi si usa l’algebra booleana.
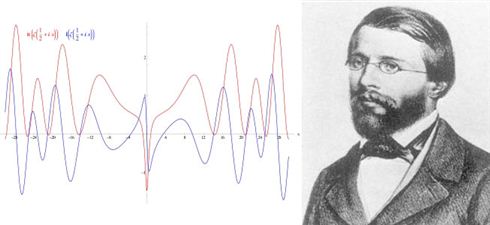
Quando invece andiamo ad effettuare una transazione elettronica ci affidiamo ad una intuizione del signore che vedete nella foto.
Non cercate questa faccia negli archivi fotografici di qualche università americana perché non la troverete.
Non è lì che dovete andare a cercare la faccia in questione, ma a Gottinga.
Dove si trova Gottinga? In Germania.
E’ a Gottinga che officiava la matematica la divinità della stessa, C.F. Gauss; è a Gottinga che insegnava matematica anche Georg Friedrich Bernhard Riemann.
Noi affidiamo la sicurezza delle nostre transazioni commerciali elettroniche alla verità della Congettura o Ipotesi di Riemann.
So cosa state pensando. Come Congettura o Ipotesi? Non è qualcosa di scientificamente provato? No, una congettura (o parimenti una ipotesi) matematica per diventare teorema deve essere provata rigorosamente.
Purtroppo non esiste il Teorema di Riemann per i Numeri Primi, esiste solo la Congettura di Riemann.
Che resiste da 150 anni.
Resiste tanto agli assalti dei matematici che vogliono dimostrarla quanto all’evidenza sperimentale.
Occorrono diversi esami universitari di matematica solo per avvicinarsi alla comprensione della funzione zeta di Riemann ζ(s) (per capire l’ipotesi di Riemann occorrerebbe conoscere alcune idee matematiche piuttosto difficili, come la funzione zeta o la geometria non-commutativa), ma diciamo che essa riguarda i numeri primi, ossia i mattoni fondamentali con i quali si costruiscono tutti i numeri; i numeri primi possono essere divisi soltanto per se stessi o per uno; ogni altro numero viene costruito moltiplicando fra loro numeri primi e ogni numero pari è la somma di due numeri primi.
Questi numeri sono ovviamente infiniti, ma nessuno è riuscito a stabilirne una qualche regolarità, in altre parole non è possibile prevedere l’andamento dei numeri primi.
Ogni volta che usiamo una carta di credito per acquistare qualcosa in rete, il nostro codice viene tenuto segreto, protetto da eventuali hackers, grazie ai numeri primi.
La crittografia elettronica utilizza come chiavi numeri interi la cui fattorizzazione in numeri primi (molto grandi) non deve essere calcolabile in tempi accettabili.
Che significa? Significa che (escludendo illeciti e tecniche criminose) per “rompere” la chiave che permette una transazione elettronica occorrerebbero un supercomputer e mesi di elaborazione.
Tutto ciò se permane la veridicità sulla Congettura di Riemann.
Qualora, per numeri straordinariamente grandi (ma grandi grandi come vedremo) non valesse più, si aprirebbe il varco (matematico prima ed informatico poi) per un attacco.
Ergo, le nostre transazioni diventerebbero esponenzialmente meno sicure di quanto non siano adesso.
Per adesso siamo al sicuro ed abbiamo a disposizione una quantità enorme di numeri primi.
Tanto per dire possiamo tranquillamente affermare, in base al Teorema di Gauss sui numeri primi, che il numero di numeri primi con 60 cifre è approssimativamente uguale a 10^60 diviso per 10^60.
A dirla in modo semplice significa che esistono abbastanza numeri primi con 60 cifre perché ogni atomo della Terra abbia la propria coppia. E non solo.
Le possibilità di vincere la lotteria nazionali sono maggiori delle probabilità che due atomi differenti sia assegnata la stessa coppia di numeri primi.
Alcuni di voi magari si staranno chiedendo: “Posto che Riemann non può aver provato a mano la sua congettura per simili numeri non è che avesse rigorosamente dimostrato la sua congettura?”.
Nessuno lo sa con esattezza, gira voce che la sua governante, nel 1866, mentre l’esercito prussiano entrava in Gottinga, abbia dato fuoco a tante carte di appunti del buon Riemann, riparato nel frattempo in Italia.
C’era la dimostrazione di Riemann in quel solerte e zelante rogo? Non lo sappiamo né lo sapremo mai.
Uno strenuo sostenitore della bontà della Congettura di Riemann è l’italiano Enrico Bombieri, un grande matematico esportato negli Stati Uniti che, insieme a gente come Atle Selberg, Peter Sarnak e Nick Katz, fa parte della cosiddetta “mafia di Princeton”. Sono loro i boss della teoria dei numeri.
Per chi volesse saperne di più mi sento di consigliare il bellissimo libro L’enigma dei numeri primi di Marcus du Sautoy. Un escursus nella materia affascinante.
Ricordo, a chi è invece più veniale, che chi riuscirà nella dimostrazione della Congettura di Riemann avrà un posto nella storia della Matematica (e non solo) e il premio da Un Milione di Dollari messo in palio dal Clay Mathematics Institute.
